Aperiodische Monokacheln

Einführung

This post is in German. If you do not understand German read this, this or that instead.

Neulich wurde ein lustiges lange bestehendes mathematisches Problem gelöst, über das ich heute schreibe. Innerhalb der kleinen Mathecommunity gibt es die Nische der Parkettierungscommunity, die sich mit Perkettierungen hauptsächlich von Ebenen beschäftigt.

Der Vorteil an Problemen in dieser Community ist, dass die Problemstellungen dort sehr visuell und intuitiv zugänglich sind um Gegensatz zu beispielsweise L-Funktionen und der Riemannschen Vermutung. Folglich eignen sie sich didaktisch perfekt für einen Einstieg in höhere Mathematik und ich werde in Zukunft auf genau diesen Blog-Artikel verweisen, wenn ich wieder gefragt werde, was ein Mathematiker eigentlich so macht, oder was in der aktuellen mathematischen Forschung passiert.

Genau aus diesem Grund ist dieser Artikel auf deutsch gehalten für ein nichttechnisches Publikum.

Parkettierungen

Eine Parkettierung ist eine Aufteilung der Ebene mit Fliesen oder Kacheln, wie im Bad. Im folgenden verwende ich Parkettierung und Kachelung synonym und nenne die einzelnen Kacheln auch manchmal Fliesen.

Das besondere an der Parkettierung ist, dass die Fliesen immer gleich sind, nur verschoben oder rotiert. Ausserdem hat eine Parkettierung keine Löcher.

Mathematisch spannend wird es, wenn nicht Bäder gefliest werden, sondern die unendlich große zweidimensionale Ebene.

In der folgenden Grafik ist ein Beispiel für eine Parkettierung mit Quadraten. Es ist nur ein Ausschnitt abgebildet. Das Parkett geht noch in alle Richtungen noch weiter.

  _ _   _ _   _ _   _ _   _ _  
|     |     |     |     |     |
|     |     |     |     |     |
| _ _ | _ _ | _ _ | _ _ | _ _ |
|     |     |     |     |     |
|     |     |     |     |     |
| _ _ | _ _ | _ _ | _ _ | _ _ |
|     |     |     |     |     |
|     |     |     |     |     |
| _ _ | _ _ | _ _ | _ _ | _ _ |
|     |     |     |     |     |
|     |     |     |     |     |
| _ _ | _ _ | _ _ | _ _ | _ _ |

Die Parkettierung ist in diesem Fall periodisch. Wenn man das ganze Parkett um eine Fliese nach rechts verschieben würde, dann würde man wieder dasselbe Muster und somit dieselbe Parkettierung erhalten. Ebenso kann man das Parkett um zwei Fliesen nach rechts verschieben. Das ist analog zu den natürlichen Zahlen.

Man könnte das Parkett auch stattdessen um eine Fliese nach oben oder unten verschieben. Oder um ein ganzzahliges Vielfaches davon.

Ebenso können diese Symmetrien kombiniert werden. Man kann das Parkett zuerst um eine Fliese nach rechts verschieben und dann um zwei Fliesen nach unten.

Interessanterweise funktioniert es auch anders herum. Jede solche Symmetrie kann man zerlegen in mehrere horizontale Verschiebungen um je eine Fliese und mehrere vertikale Verschiebungen um eine Fliese.

Dies ist ähnlich zur Primfaktorzerlegung einer Zahl. Jede ganze Zahl kann eindeutig (bis auf Vorzeichen und Reihenfolge) in mehrere Primzahlen zerlegt werden. Man würde sagen, dass die horizontale und die vertikale Verschiebung erzeugende Elemente der Symmetriegruppe sind.

Ebenso könnte man eine andere Parkettierung betrachten:

  _ _   _ _   _ _   _ _   _ _  
|     |     |     |     |     |
|     |     |     |     |     |
| _ _ | _ _ | _ _ | _ _ | _ _ | _
   |     |     |     |     |     |
   |     |     |     |     |     |
 _ | _ _ | _ _ | _ _ | _ _ | _ _ |
|     |     |     |     |     |
|     |     |     |     |     |
| _ _ b _ _ | _ _ | _ _ | _ _ | _
   |     |     |     |     |     |
   |     |     |     |     |     |
   a _ _ | _ _ | _ _ | _ _ | _ _ |

Hier kann man wieder das Parkett horizontal um eine Fliese verschieben. Ebenso ist es aber auch möglich das Parkett schräg nach rechts oben zu verschieben, sodass der Punkt (a) auf den Punkt (b) abgebildet wird.

Eine Kachelung kann auch aus mehreren verschiedenen kacheln bestehen. Betrachtet man das unten abgebildete Pentagon

    _ _   
  /     \ 
 /       \
 \       /
  \ _ _ / 

… und die unten abgebildete Raute

 / \ 
/   \
\   /
 \ /

… kann man damit das folgende Parkett erzeugen:

    _ _       _ _       _ _       _ _   
  /     \   /     \   /     \   /     \ 
 /       \ /       \ /       \ /       \
 \       / \       / \       / \       /
  \ _ _ /   \ _ _ /   \ _ _ /   \ _ _ /
  /     \   /     \   /     \   /     \
 /       \ /       \ /       \ /       \
 \       / \       / \       / \       /
  \ _ _ /   \ _ _ /   \ _ _ /   \ _ _ /
  /     \   /     \   /     \   /     \
 /       \ /       \ /       \ /       \
 \       / \       / \       / \       /
  \ _ _ /   \ _ _ /   \ _ _ /   \ _ _ /
  /     \   /     \   /     \   /     \
 /       \ /       \ /       \ /       \
 \       / \       / \       / \       /
  \ _ _ /   \ _ _ /   \ _ _ /   \ _ _ /

Auch hier gibt es wieder verschiedene Symmetrien. Es ist anzumerken, dass Kacheln in der Mathematik verschoben, gespiegelt und rotiert werden dürfen. Die Fliesen im Bad sollten im Allgemeinen nicht gespiegelt werden.

Nichtperiodische Parkettierungen

Eine naheliegende Frage ist, ob es Parkettierungen gibt, die keine Symmetrien haben. Solche Parkettierungen nennt man nichtperiodisch.

Man könnte hierzu eine Zahlenfolge nehmen, die keine Periodizität hat und diese dann in die Kacheln geeignet kodieren. Zum Beispiel könnte man ein quadratisches Grundgitter nehmen und durchzählen. Jedes Quadrat, das auf einer Primzahlposition ist, könnte man horizontal teilen und alle anderen Quadrate vertikal.

0      1     2     3     4     5     6     7     8     9     10    11    12
  _ _   _ _   _ _   _ _   _ _   _ _   _ _   _ _   _ _   _ _   _ _   _ _   _ _  
|     |     |  |  |  |  |     |  |  |     |  |  |     |     |     |  |  |     |
| - - | - - |  |  |  |  | - - |  |  | - - |  |  | - - | - - | - - |  |  | - - |
| _ _ | _ _ | _|_ | _|_ | _ _ | _|_ | _ _ | _|_ | _ _ | _ _ | _ _ | _|_ | _ _ |

Diese Parkettierung hat keine Symmetrien, weil die Primzahlen keine Symmetrien haben. Man könnte das Gitter vermutlich noch geeignet nach unten ausdehnen auf die zweite Dimension, dass auch dort keine Symmetrien auftauchen.

Nichtperiodische Parkettierungen sind einfach zu bauen. Viel lustiger sind die aperiodischen Fliesen.

Aperiodische Fliesen

Die Frage nach nichtperiodischen Parkettierungen ist ob man die ebene mit einer Fliese so parkettieren kann, dass es keine Periodizität gibt. Es handelt sich dabei um die Frage nach einer Parkettierung.

Die Frage nach aperiodischen Fliesen ist, ob es eine Kachel gibt, mit der man die Ebene so parkettieren kann, dass die entstehenden Parkettierungen immer nichtperiodisch sind.

Man nennt dann sowohl die Fliesen, als auch die Parkettierungen aperiodisch. Aber eigentlich würde es mehr Sinn ergeben nur die Fliese(n) aperiodisch zu nennen.

Penrose Parkettierung

Penrose Parkettierungen sind die einfachsten Beispiele für aperiodische Kacheln. Es gibt mehrere Penrose Parkettierungen. Penrose Parkettierungen bestehen immer aus zwei verschiedenen Formen und es ist unmöglich die Ebene damit periodisch zu kacheln. Diese Parkettierungen wurden nicht, wie man annehmen könnte im antiken Griechenland entdeckt, sondern erst in den 1970er Jahren. Bis dahin waren gar keine aperiodischen Fliesen bekannt.

Hier ein Beispiel für eine Penrose Parkettierung:

Diese Parkettierung hat eine Rotationssymmetrie, aber das ist erlaubt. Nur Periodizität, also Symmetrien basierend auf Verschiebungen sind verboten.

Die Penrose Parkettierung ist zwar eine aperiodische Parkettierung, aber eigentlich wäre es ästhetischer, wenn man nur eine Kachelform hätte. Wenn man zum Beispiel Plätzchen bäckt, muss man nun aufpassen, dass man von beiden Plätzchenformen gleich viele produzieren muss.

Socolar-Taylor Kachel

Die Idee hinter der Socolar-Taylor Kachel ist, dass man eine Grundfläche aus Sechsecken nimmt. An diese Sechsecke werden nun lustige Nasen und Kerben angebaut, die erzwingen, das diese auf eine bestimmte Art ausgelegt werden müssen, die Nichtperiodizität erzwingt. Werden die Kacheln anders ausgelegt, so werden die Kerben nicht mit Nasen ausgefüllt, oder es verbleiben Löcher.

Eine Kachelung mit der Socolar-Taylor Kachel sieht wie folgt aus:

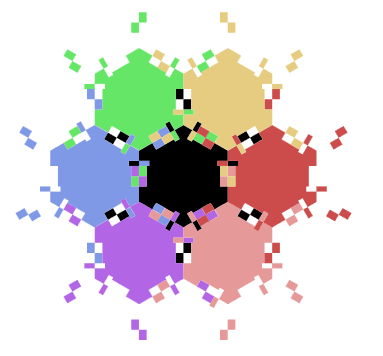
Hierbei ist jede Kachel in einer Farbe.

Das Problem daran ist, dass diese Kachel unzusammenhängend ist. Die Quadrate die nicht mit der Kachel verbunden sind, müssen immer gleich mit der Kachel mitbewegt werden, deswegen handelt es sich von der Definition her um eine Kachel. Aber es ist nicht ästhetisch.

Unzusammenhängende aperiodische Kacheln sind nützlich für Graffiti auf Uni-Toiletten oder Tätowierungen, aber man kann damit wiederum keine Plätzchen backen oder lustige Legespiele aus Holz bauen

Jahrhundertproblem

Kommen wir nun zum eigentlichen Problem, das neulich gelöst wurde.

Die Frage ist nach einer aperiodischen Kachel: Gibt es eine zusammenhängende Kachelform, sodass egal wie man die Ebene damit parkettiert, das entstehende Muster nicht periodisch ist?

Oder anders formuliert: Gibt es eine aperiodische Monokachel?

Vielleicht gibt es auch gar keine solche Kachel und man kann beweisen, dass es sie nicht gibt. Das war aber nicht der Fall. Neulich wurde eine Kachel mit diesen Eingenschaften von David Smith, Joseph Samuel Myers, Craig S. Kaplan und Chaim Goodman-Strauss entdeckt. Es wurden sogar zwei Kacheln entdeckt, die jeweils für sich aperiodisch sind.

Die eine ist als Hut (hat) bekannt, obwohl sie eher aussieht wie ein Shirt. Die andere hat den Nicknamen Schildkröte (turtle) bekommen.

Wenn man die Socolar-Taylor Kachel aus dem letzten Abschnitt gesehen hat, würde man denken, dass die aperiodische Monokachel noch viel grimmiger aussehen würde. Das war aber nicht der Fall.

Die beiden Kacheln sehen wie folgt aus. In der linken Spalte befindet sich der Hut und in der rechten Spalte die Schildkröte.

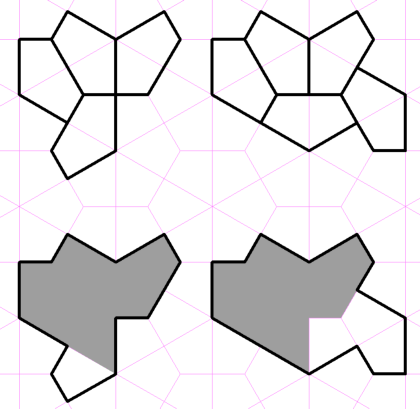
Eine Kachelung mit Hüten sieht wie folgt aus:

Anwendungen

Anwendungen hat das angeblich in der Physik, wenn es um die Struktur von Kristallen oder Quasikristallen geht. Aber ich bin kein Physiker und bin eher an der platonischen Welt der Ideen interessiert. Welche Anwendung hat ein Gedicht? Welche Anwendung hat ein Gemälde von Escher?

Kachelkult

Anbei noch ein Bild von Craig Kaplan, der mit seinem Team die Aperiodizität der Kachel bewiesen hat.

Ich persönlich halte Bilder von den Leuten für egal, obwohl im Wissenschaftsjournalismus immer die Leute gezeigt werden. Wieso ich das Bild hier zeige ist wegen dem großartigen Regal.

Alleine schon die dreidimensionale Hilbertkurve in der dritten Reihe oder die Origamistücke, die lustig zu Sternen zusammengesetzt wurden. Gäbe es ein Abo, bei dem man jeden Monat einen solchen Gegenstand geschickt bekommen würde, würde ich jeden Preis dafür zahlen! Am besten noch als Bausatz.

Wie dem auch sei. Auf jeden Fall kann man nun die aperiodische Monokachel als Plätzchenausstecherform bauen. Bei den Penrose Kacheln benötigte man zwei verschiedene Formen. Hier benötigt man allerdings auch zwei Formen, wenn man es sauber machen will, da die gespiegelte Form des Plätzchens dann doch etwas anders aussieht, als wenn man das Plätzchen einfach umdreht.

Es handelt sich jetzt hierbei um den Hut. Nicht um die Schildkröte.

Danksagungen

• @ntumanov_Xray für das Erstellen der Vorlage für die Ausstecherleform.
• einem Arbeitskollegen ohne Internetpräsenz für das Drucken meiner Ausstecherleform.