Pricing Continuous Barrier Options

Introduction

In this post we are going to take a look at continuous barrier options. These are options which are activated or deactivated when crossing a predetermined price barrier. We will explain the In-Out-parity and compute the expected payoff.

Definitions

A continuous barrier option is an option on an underlying that pays out (or does not pay out) depending on if the underlying has crossed a price barrier. Once crossing that barrier and being activated (deactivated), the option does not deactivate (activate) again. The payouts can be european style, american style, bermudan style, or some other stuff.

In particular there are four flavors of continuous barrier options:

• Up-and-out: Here the price of the underlying starts below the barrier level and becomes invalid (knocked out, in trader geekspeak) if it crosses that level.

• Down-and-out: Here the price of the underlying starts above the barrier level and is knocked out when falling below that threshold.

• Up-and-in: The price of the underlying starts below the barrier level and becomes activated (knocked in) when crossing that level.

• Down-and-in: As one would expect, here spot price starts above the barrier level. When it crosses the barrier it is knocked in.

Advantages

Why should you trade that stuff? Isn’t this some wall-street gambler tool?
It depends. You can of course use it as a gambler tool if you don’t blame me when you lose. Normally, one considers buying continuous barrier options in the same situation where one considers buying vanilla options, namely when using them to hedge a portfolio. In case they get knocked in, they work like a vanilla option, so they can be used as an insurance against price bumps.

Continuous barrier options have the advantage that they are cheaper than their vanilla counterparts. As you can see, they will pay at most the value of their vanilla counterpart, so their price is at most the price of the vanilla option (in an arbitrage-free world).

In-out-parity

With european options we saw that there is a parity between the put and the call which helped us to reduce the price of the call to the price of the put, so we only needed to compute one of them.

It turns out, that with continuous barrier options there is a similar parity, called the In-Out-parity. Assume we are holding two continuous barrier options with the same barrier level. For the argument it does not matter if these are puts or calls. One of these options is an X-and-in-option \(O_{in}\) the other is an X-and-out-option \(O_{out}\). Now two things can happen:

1. If we are below the barrier at expiry time, then one of the options is valid and pays according to the corresponding vanilla option \(O\), whereas the other barrier option is invalid and pays nothing.

2. In contrast, if we are above the barrier level at expiry time, the reverse happens. The option which paid out before now pays out nothing, and the other option pays according to the vanilla option \(O\).

So, in both cases we get \(\begin{align*} O_{in}+O_{out}=O \end{align*}\)

In plain language this means, that if you hold a knock in option and the corresponding knock out option, then both together are knockless, which is perhaps a word i made up.

Again as with european options the parity makes life easier. If we know the price of the up-and-out option \(O_{out}\) and of the vanilla option \(O\) we can compute the price of the up-and-in option \(O_{in}\).
This also works the other way: if we know the price of the up-and-in option \(O_{in}\) and the vanilla option \(O\) and want to know the price of \(O_{out}\). It also works analogously for down-and-X options.

Pricing

How do we price these monsters? As with other options, we can take the Black-Scholes differential equation and solve for the boundary condition of the payoff of a continuous barrier option. Another possibility is the martingale pricing approach.

What we will do in the following is the easiest and slowest approach, namely Monte-carlo pricing. We will simulate many runs of the underlying asset assuming their spot price follows a geometric brownian motion.

To make life easier, we will only compute european continuous barrier call options. W.l.o.g. we are concentrating on an up-and-out option. Note that the price of the up-and-in option can be computed with the In-Out-parity.

import numpy as np
import matplotlib.pyplot as plt 

# Defining the relevant functions

def geometric_brownian_motion(N = 200, T = 1, S_0 = 1, mu=0.08, sigma = 0.05):
        """N is the number of steps, T is the time of expiry,
        S_0 is the beginning value, sigma is standard deviation"""
        deltat = float(T)/N #compute the size of the steps
        W = np.cumsum(np.random.standard_normal(size = N)) * np.sqrt(deltat)
        # generate the brownian motion
        t = np.linspace(0, T, N)
        X = (mu-0.5*sigma**2)*t + sigma*W
        S = S_0 * np.exp(X)
        # geometric brownian motion
        return S

def european_call_payoff(S_T, K = 1.5):
        """S_T is the price of the underlying at expiry.
        K is the strike price"""
        return np.maximum(0, S_T - K) #payoff for call option

def price_up_and_out_european_barrier_call(barrier, S_0, N = 500, K = 0.5):
        """barrier is the barrier level,
        S_0 is the starting value of the underlying,
        N is how many paths we will generate to take the mean.
        K is the strike price."""
        paths = [geometric_brownian_motion(S_0 = S_0) for i in range(N)]
        prices = []
        for path in paths:
                if np.max(path) > barrier: # knocked out
                        prices.append(0)
                else:
                        prices.append(european_call_payoff(path[-1], K)) 
        return np.mean(prices)


# Simulating the price depending on the current spot
# barrier is at 2.5
# strike price is at 0.5

spot = np.linspace(0, 3, 100)
prices = [price_up_and_out_european_barrier_call(2.5, s) for s in spot]
plt.plot(spot, prices, '--', linewidth=2)
plt.show()

Before showing the image, let us discuss what we expect.

We have an up-and-out call option with barrier of \(2.5\) and strike price \(0.5\). We compute the expected payoff for all spots of the underlying between \(0\) and \(3\). On the x-axis we get the spots and on the y-axis the expected payoffs.

First, somewhere left of \(0.5\), the expected payoff should be zero, since the call option there is zero and the asset will not move with high probability enough to the right, such that the call option pays out.

Right of \(2.5\) the expected payoff is zero, since we have crossed the barrier and thus the continuous barrier option is knocked out.

In between, we see the expected payoff of the call option and the more to the left we go, the smaller will be the influence of the barrier.

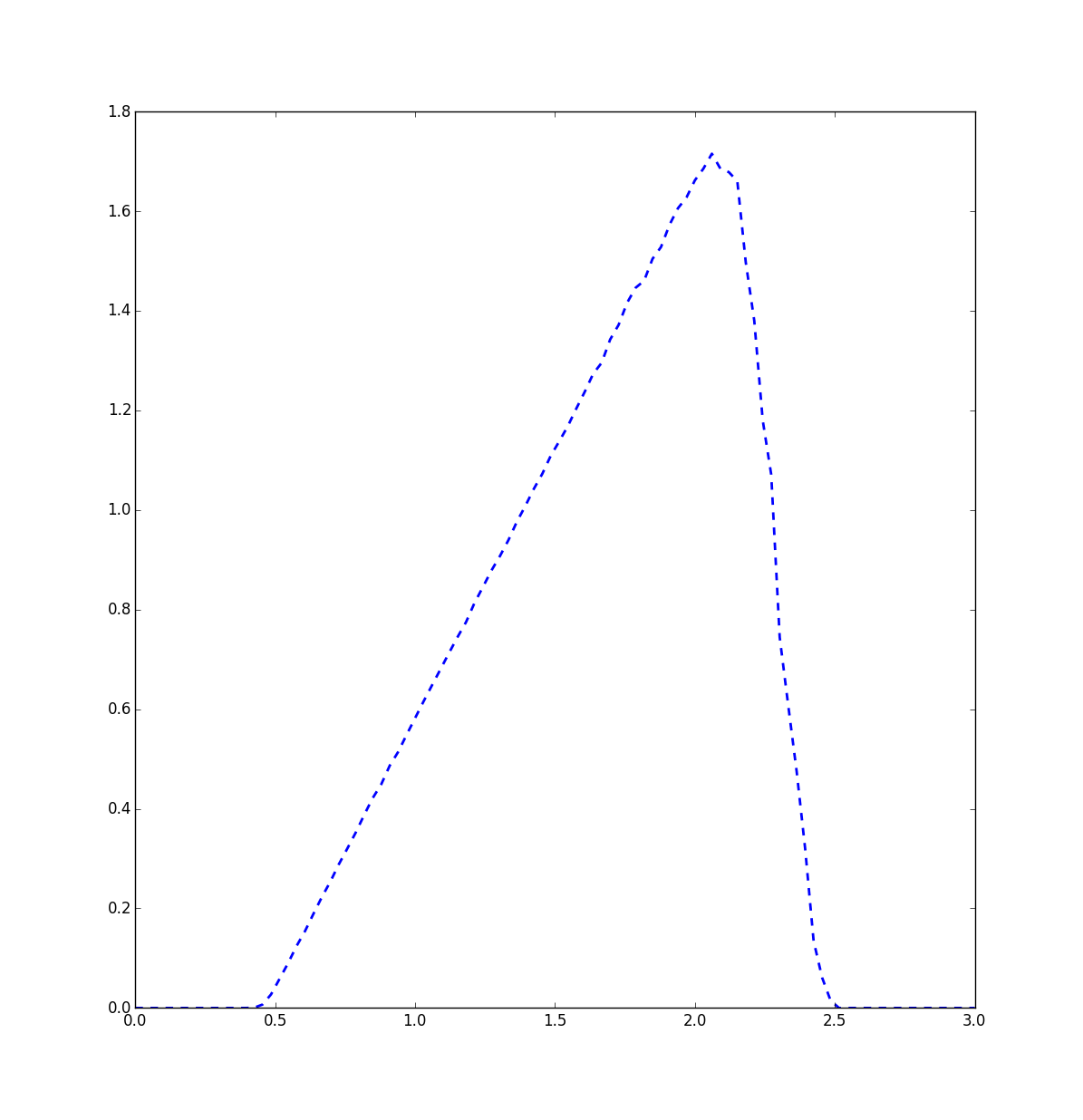
To get the price of the barrier option, we have to discount the interest rate. This is left as a small exercise.

Practical problems

In practice there often is a problem with determining if the price of the underlying has crossed the barrier level. Concretely, which price do we take? The bid or the ask? The midpoint? What happens when the spot price crosses the barrier level, but is not traded at this price?

Because of these problems in practice one often does not have continuous barrier options but rather discrete barrier options, which take the prices of the close at the end of the day for determining if they have crossed the barrier.